Introduction

Example

Analysis

Practical Implementations

Introduction

Bubble sort is one of the simplest sorting algorithms available, and perhaps as a consequence one of the worst.

The name gives some indication of how the technique works - each item bubbles it’s way up the list into it’s proper sorted place. The process is in the general case very slow, but does have some potential in certain cases.

The procedure for bubble sort is as follows. Compare the first two items in the list. If they are in the wrong order, swap them around. Compare now the second and third item. Again, swap them into the correct order if necessary. Now compare the third and fourth items, etc. After a complete pass in this way, each item is slightly closer to it's correct position in the final ordering.  More definitively, the last item will in fact always be in the correct position.  After the second pass, the last two items will be in their correct positions.  As for after the third, etc.

Thus the sort can take up to (N-1) passes to complete.  If you're thinking it should take N passes, remember that when you get down to two items, and you know one is in the right position, then of course the other one must be too.  Thus, N-1.

Introduction

Example

Analysis

Practical Implementations

Example

As an illustration, consider the following list of items.

If we now apply the bubble sort method, we can see this list become sorted into ascending order, left to right.

First of all the first two elements, 9 and 4, are compared.  Clearly 4 is less than 9, so they are swapped.

Now 9 and 5 are compared, and swapped.

Now 9 and 1 are compared, and swapped.

And finally 9 and 7 are compared, and swapped.

That completes one pass, with the list seen as above.  It's obvious at this point that the 1 need only be moved to the start of the list in order to complete the sort.  But bubble sort doesn't pick this up, and so it takes another two passes, shown below, before the list is finally sorted.  Note however that these passes are successively shorter than the first, because the 2nd pass need only compare the first 4 items, and the 3rd the first 3.

As so we finally have the listed sorted.  And we only did 3 passes, not the 4 we might have had to do, had the (1) been the last item to start with - try this worst-case scenario on paper for yourself, as shown below.

As you can see, as the list gets bigger, each pass takes longer, and there's more of them.  Thus, for a list of twice the size, you'll inevitably end up doing more than twice the work.  If we look at all this mathematically, we can find out precisely just how disastrous bubble sort is.

Introduction

Example

Analysis

Practical Implementations

Analysis

Let's assume each sort requires all n-1 passes.  This is, as in the previous example, not usually true.  But it is much simpler to analyze, while remaining still meaningful, as some real world implementations do actually do all n-1 passes regardless.  As it turns out, sometimes it's not worth your time checking whether you've finished early, because this simple check can make the sort significantly slower!  If you are fairly confident your data will be very jumbled up, it's quite often better to just do the n-1 sorts regardless, rather than keep hoping for a significantly better-than-average case.

Now, on the first pass you perform N-1 comparisons.  On the second you perform N-2... on the third N-3, etc.  So, some simple maths will show that on average you perform N/2 comparisons per pass.  So the total number of comparisons will be (N-1)(N/2), most often written as (1/2)(N^2)-(1/2)N.

As you can see, as soon as you get any significant number of items in your list, the number of comparisons you'll have to do is enormous.  Consider for one final example a list of one million items.  That would require just under half a million million comparisons (4.99 x 10^11).

Of course, comparisons aren't the only noticeable operation - there's also many swaps performed.  Swaps are usually only as intensive as swapping two pointers around, so compared to comparisons they're usually lesser concerns.  However, as we'll see there are a lot of them made in bubble sort, so they are still a significant factor.

How many swaps do you do on each pass?  Well, that depends, of course.  You could do n-1, if the first element should in fact be the last.  Or you could do none, if the list is completely sorted.  Proving how many mathematically is surprisingly difficult.  I won't go through the details here, but ultimately you end up with the mathematical proof below, showing the average number of swaps required to sort a list containing n items is given by:

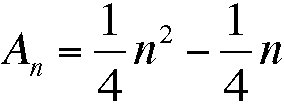
In tabular form, this works as follows:

So, we can now begin to consider the performance of bubble sort as a whole.  This is where it gets trickier, because you need to decide how much harder or easier a swap is than a comparison.  To start with, let's assume they're the same.  Thus, the average time to sort a list is:

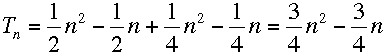
As you can see, this is a pretty bad average case.  For 1,000,000 items, that's 3/4 of a million million time units.  Even if we're talking time units measured as single microseconds, that translates to a total time of 3/4 of a million seconds!  That's nearly 9 hours - not a great scenario.  And in case you're thinking modern computers are way faster than that, think again - memory bandwidth and latencies play the main part in large lists, and result in even simple comparison and swaps taking on the order of a microsecond each.

Now, if your comparisons are much faster than your swaps, you'll see better performance than the other way around, where your comparisons are slower.  This is because of the obvious fact that you, on average, do twice as many comparisons as swaps.

So that's the performance of bubble sort; of the order O(n^2).  This is about as bad as sorting algorithms get.  Better algorithms (i.e. just about anything) offer speeds in the order of O(nlog2(n)), O(n), or even O(log2(n)).

It should be mentioned that what has been considered so far is only the average case.  In the best case - an already sorted list - you would not perform any swaps.  In the worst case, you would perform a swap for each comparison, and so would have a time expression of (N^2)-N.  Eek!

Introduction

Example

Analysis

Practical Implementations

Practical Implementations

There are several ways to implement bubble sort.  For starters, we'll consider the simplest form.  The first version of performBubbleSort() works on a generic integer array, and gives you a good simple view of how bubble sort works.  The second is more like what you'd use for sorting a STL vector containing complex objects.

void performBubbleSort(int array[], int size) {
   int i, j, swapTemp;

   for (i = size; i > 1; --i) { // n - 1 passes
     for (j = 1; j < i; ++j) { // n - 1 comparisons per pass
       if (array[j] < array[j - 1]) { // comparison
         swapTemp = array[j]; // swap
         array[j] = array[j - 1];
         array[j - 1] = swapTemp;
       }
     }
   }
}

template<class V, class A> void performBubbleSort(vector<V*, A> &vec) {
   int rearOffset = 1;
   typename vector<V*, A>::iterator lastItem, iterator;

   while ((lastItem = vec.end() - rearOffset++) != vec.begin()) {
     for (iterator = vec.begin(); iterator < lastItem; ++iterator) {
       if (*(*iterator) > *(*(iterator + 1))) {
         swap(*iterator, *(iterator + 1));
       }
     }
   }
}

There are several ways of potentially improving the speed of bubble sort.  As has been mentioned previously, you won't always have to perform n-1 passes.  If you think your large list is going to be somewhat ordered to start with (like the graphical example at the top of this page), you may only need some fraction of n passes.  And if you remember the table from before, even just reducing the number of passes by a quarter could nearly double the speed of your sort.  But more significantly, if the list is already sorted, your best case becomes a simple case of N-1 comparisons, and no swaps.  That puts the sort on the order of O(n), which is relatively excellent.  The worst case, however, is still (N^2)-N swaps & comparisons.

You can find the last pass by simply finding the first pass in which you don't swap anything.  If you haven't swapped anything, everything must obviously be in order.  So, the two previous examples have been altered to detect this:

void performBubbleSort(int array[], int size) {
   int i, j, swapTemp;
   bool didPerformSwap = true;

   for (i = size; (i > 1) && didPerformSwap; --i) { // n - 1 passes
     didPerformSwap = false;

     for (j = 1; j < i; ++j) { // n - 1 comparisons per pass
       if (array[j] < array[j - 1]) { // comparison
         didPerformSwap = true;
         swapTemp = array[j]; // swap
         array[j] = array[j - 1];
         array[j - 1] = swapTemp;
       }
     }
   }
}

template<class V, class A> void performBubbleSort(vector<V*, A> &vec) {
   int rearOffset = 1;
   typename vector<V*, A>::iterator lastItem, iterator;
   bool didPerformSwap = true;

   while (((lastItem = vec.end() - rearOffset++) != vec.begin()) && didPerformSwap) {
     didPerformSwap = false;

     for (iterator = vec.begin(); iterator < lastItem; ++iterator) {
       if (*(*iterator) > *(*(iterator + 1))) {
         didPerformSwap = true;
         swap(*iterator, *(iterator + 1));
       }
     }
   }
}

For the average case, the modified method only does half the passes, so it is 33% faster.  Not 50%!  This is because on average you don't do the last N/2 passes.  But these passes are short anyway, because by then you've already sorted half the list, so they don't account for half the time - only a third.

Mathematically, the first half of the passes deal with (N-1) through to (N-(N/2)) items.  The average of these is of course roughly (3/4)N, not (1/2)N as before.  So while the number of passes is reduced to approximately (N-1)/2, the average number of comparisons for these passes is increased as mentioned, and thus the average number of comparisons becomes (3/8)N(N-1), versus the (1/2)N(N-1) we had previously.  So, just 33% faster.  But still, that is a good improvement.  Combined with further optimizations, it builds up an overall significant improvement.

Introduction

Example

Analysis

Practical Implementations